BatchNormalization原理与python实现

背景

炼丹困扰

在深度学习中，由于问题的复杂性，我们往往会使用较深层数的网络进行训练，需要去尝试不同的学习率、初始化参数方法（例如Xavier初始化）等方式来帮助我们的模型加速收敛。

深度神经网络之所以如此难训练，其中一个重要原因就是网络中层与层之间存在高度的关联性与耦合性。

网络中层与层之间的关联性会导致如下的状况：随着训练的进行，网络中的参数也随着梯度下降在不停更新。

一方面，当底层网络中参数发生微弱变化时，由于每一层中的线性变换与非线性激活映射，这些微弱变化随着网络层数的加深而被放大（类似蝴蝶效应）；
另一方面，参数的变化导致每一层的输入分布会发生改变，进而上层的网络需要不停地去适应这些分布变化，使得我们的模型训练变得困难。这一现象叫做Internal Covariate Shift。

Internal Covariate Shift

一个较规范的定义：在深层网络训练的过程中，由于网络中参数变化而引起内部结点数据分布发生变化的这一过程被称作Internal Covariate Shift。

我们定义每一层的线性变换为 $Z^{[l]}=W^{[l]}\times input+b^{[l]}$ ，其中 $l$ 代表层数；非线性变换为 $A^{[l]}=g^{[l]}(Z^{[l]})$ ，其中 $g^{[l]}(\cdot)$ 为第 $l$ 层的激活函数。

随着梯度下降的进行，每一层的参数 $W^{[l]}$ 与 $b^{[l]}$ 都会被更新，那么 $Z^{[l]}$ 的分布也就发生了改变，进而 $A^{[l]}$ 也同样出现分布的改变。而 $A^{[l]}$ 作为第 $l+1$ 层的输入，意味着 $l+1$ 层就需要去不停适应这种数据分布的变化。

Internal Covariate Shift带来的问题

（1）上层网络需要不停调整来适应输入数据分布的变化，导致网络学习速度的降低

我们在上面提到了梯度下降的过程会让每一层的参数 $W^{[l]}$ 和 $b^{[l]}$ 发生变化，进而使得每一层的线性与非线性计算结果分布产生变化。后层网络就要不停地去适应这种分布变化，这个时候就会使得整个网络的学习速率过慢。

（2）网络的训练过程容易陷入梯度饱和区，减缓网络收敛速度

当我们在神经网络中采用饱和激活函数（saturated activation function）时，例如sigmoid，tanh激活函数，很容易使得模型训练陷入梯度饱和区（saturated regime）。

随着模型训练的进行，我们的参数 $W^{[l]}$ 会逐渐更新并变大，此时 $Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]}$ 就会随之变大，并且 $Z^{[l]}$ 还受到更底层网络参数 $W^{[1]},W^{[2]},\cdots,W^{[l-1]}$ 的影响，随着网络层数的加深， $Z^{[l]}$ 很容易陷入梯度饱和区，此时梯度会变得很小甚至接近于0，参数的更新速度就会减慢，进而就会放慢网络的收敛速度。

对于激活函数梯度饱和问题，有两种解决思路：

第一种就是更为非饱和性激活函数，例如线性整流函数ReLU可以在一定程度上解决训练进入梯度饱和区的问题。另一种思路是，我们可以让激活函数的输入分布保持在一个稳定状态来尽可能避免它们陷入梯度饱和区，这也就是Normalization的思路。

Batch Normalization

思路

尝试单独对每个特征进行normalizaiton就可以了，让每个特征都有均值为0，方差为1的分布即可。在mini-batch的基础上进行计算。

算法步骤

介绍算法思路沿袭前面BN提出的思路来讲。第一点，对每个特征进行独立的normalization。我们考虑一个batch的训练，传入m个训练样本，并关注网络中的某一层，忽略上标 $l$ 。

$Z\in \mathbb{R}^{d_l\times m}$

我们关注当前层的第 $j$ 个维度，也就是第 $j$ 个神经元结点，则有 $Z_j\in \mathbb{R}^{1\times m}$ 。我们当前维度进行规范化：

$\mu_j=\frac{1}{m}\sum_{i=1}^m Z_j^{(i)}$

$\sigma^2_j=\frac{1}{m}\sum_{i=1}^m(Z_j^{(i)}-\mu_j)^2$

$\hat{Z}_j=\frac{Z_j-\mu_j}{\sqrt{\sigma_j^2+\epsilon}}$

其中 $\epsilon$ 是为了防止方差为0产生无效计算。

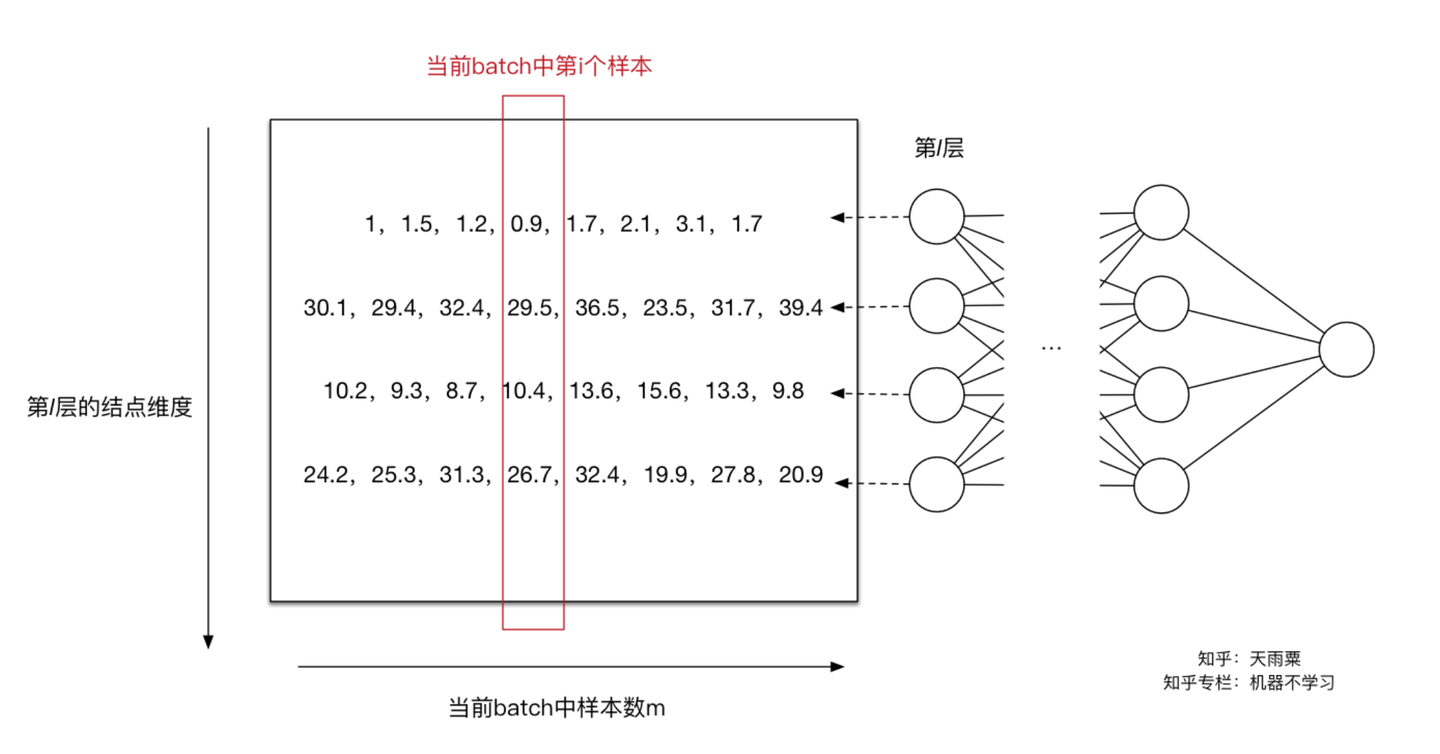
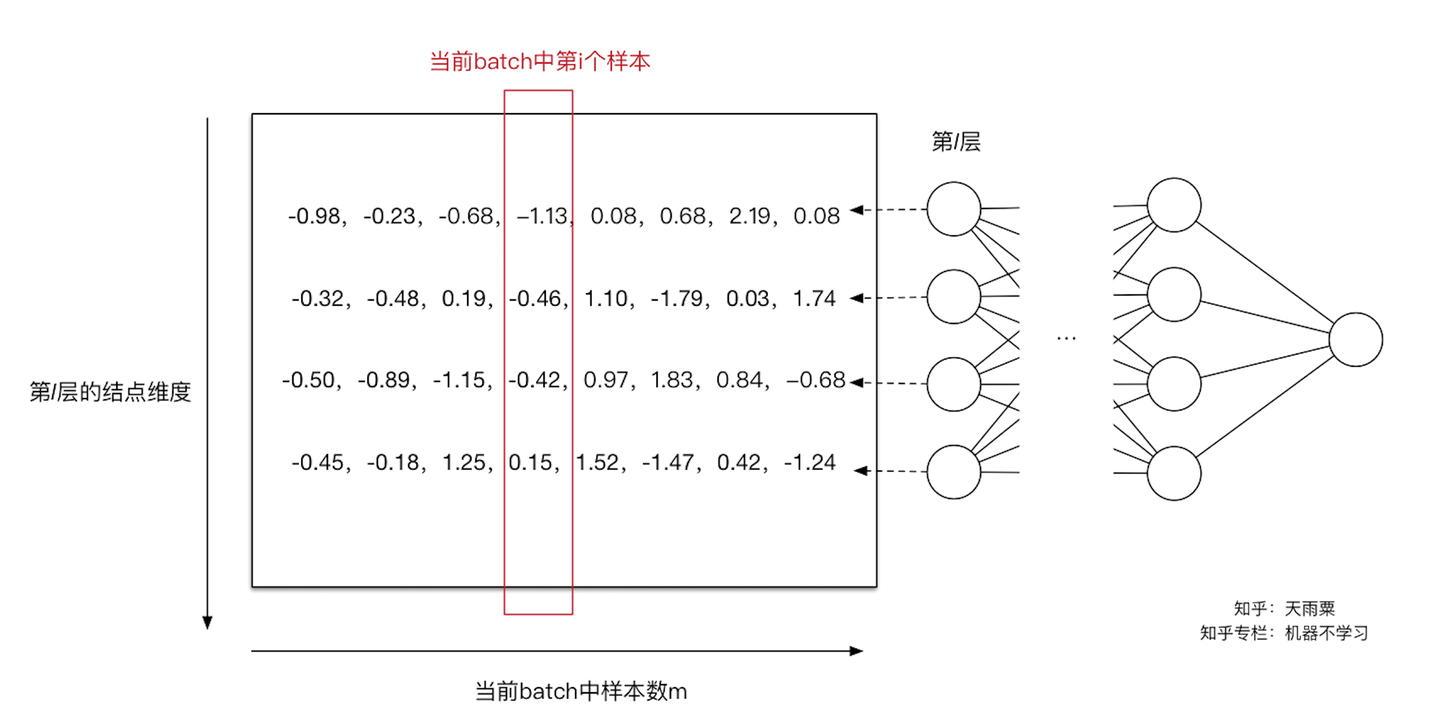
通过上面的变换，我们解决了第一个问题，即用更加简化的方式来对数据进行规范化，使得第 $l$ 层的输入每个特征的分布均值为0，方差为1。

如同上面提到的，Normalization操作我们虽然缓解了ICS问题，让每一层网络的输入数据分布都变得稳定，但却导致了数据表达能力的缺失。也就是我们通过变换操作改变了原有数据的信息表达（representation ability of the network），使得底层网络学习到的参数信息丢失。

另一方面，通过让每一层的输入分布均值为0，方差为1，会使得输入在经过sigmoid或tanh激活函数时，容易陷入非线性激活函数的线性区域。

因此，BN又引入了两个可学习（learnable）的参数 $\gamma$ 与 $\beta$ 。

这两个参数的引入是为了恢复数据本身的表达能力，对规范化后的数据进行线性变换，即 $\tilde{Z_j}=\gamma_j \hat{Z}_j+\beta_j$ 。特别地，当 $\gamma^2=\sigma^2,\beta=\mu$ 时，可以实现等价变换（identity transform)并且保留了原始输入特征的分布信息。通过上面的步骤，我们就在一定程度上保证了输入数据的表达能力。

训练时，均值、方差分别是该批次内数据相应维度上的均值与方差；训练一旦结束，学习参数gamma和bata也就确定了。

以上就是整个Batch Normalization在模型训练中的算法和思路。

计算公式

对于神经网络中的第 $l$ 层，我们有：

$Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]}$

$\mu=\frac{1}{m}\sum_{i=1}^mZ^{[l](i)}$

$\sigma^2=\frac{1}{m}\sum_{i=1}^m(Z^{[l](i)}-\mu)^2$

$\tilde{Z}^{[l]}=\gamma\cdot\frac{Z^{[l]}-\mu}{\sqrt{\sigma^2+\epsilon}}+\beta$

$A^{[l]}=g^{[l]}(\tilde{Z}^{[l]})$

测试阶段使用BatchNormalization

利用BN训练好模型后，我们保留了每组mini-batch训练数据在网络中每一层的 $\mu_{batch}$ 与 $\sigma^2_{batch}$ 。此时我们使用整个样本的统计量来对Test数据进行归一化，具体来说使用均值与方差的无偏估计：

$\mu_{test}=\mathbb{E} (\mu_{batch})$

$\sigma^2_{test}=\frac{m}{m-1}\mathbb{E}(\sigma^2_{batch})$

得到每个特征的均值与方差的无偏估计后，我们对test数据采用同样的normalization方法：

$BN(X_{test})=\gamma\cdot \frac{X_{test}-\mu_{test}}{\sqrt{\sigma^2_{test}+\epsilon}}+\beta$

Batch Normalization的优势

Batch Normalization在实际工程中被证明了能够缓解神经网络难以训练的问题，BN具有的优势可以总结为以下三点：

（1）BN使得网络中每层输入数据的分布相对稳定，加速模型学习速度

BN通过规范化与线性变换使得每一层网络的输入数据的均值与方差都在一定范围内，使得后一层网络不必不断去适应底层网络中输入的变化，从而实现了网络中层与层之间的解耦，允许每一层进行独立学习，有利于提高整个神经网络的学习速度。

（2）BN使得模型对网络中的参数不那么敏感，简化调参过程，使得网络学习更加稳定

在神经网络中，我们经常会谨慎地采用一些权重初始化方法（例如Xavier）或者合适的学习率来保证网络稳定训练。

当学习率设置太高时，会使得参数更新步伐过大，容易出现震荡和不收敛。但是使用BN的网络将不会受到参数数值大小的影响。例如，我们对参数 $W$ 进行缩放得到 $aW$ 。对于缩放前的值 $Wu$ ，我们设其均值为 $\mu_1$ ，方差为 $\sigma^2_1$ ；对于缩放值 $aWu$ ，设其均值为 $\mu_2$ ，方差为 $\sigma^2_2$ ，则我们有：

$\mu_2=a\mu_1$ ， $\sigma^2_2=a^2\sigma^2_1$

我们忽略 $\epsilon$ ，则有：

$BN(aWu)=\gamma\cdot\frac{aWu-\mu_2}{\sqrt{\sigma^2_2}}+\beta=\gamma\cdot\frac{aWu-a\mu_1}{\sqrt{a^2\sigma^2_1}}+\beta=\gamma\cdot\frac{Wu-\mu_1}{\sqrt{\sigma^2_1}}+\beta=BN(Wu)$

$\frac{\partial{BN((aW)u)}}{\partial{u}}=\gamma\cdot\frac{aW}{\sqrt{\sigma^2_2}}=\gamma\cdot\frac{aW}{\sqrt{a^2\sigma^2_1}}=\frac{\partial{BN(Wu)}}{\partial{u}}$

$\frac{\partial{BN((aW)u)}}{\partial{(aW)}}=\gamma\cdot\frac{u}{\sqrt{\sigma^2_2}}=\gamma\cdot\frac{u}{a\sqrt{\sigma^2_1}}=\frac{1}{a}\cdot\frac{\partial{BN(Wu)}}{\partial{W}}$

注：公式中的 $u$ 是当前层的输入，也是前一层的输出

我们可以看到，经过BN操作以后，权重的缩放值会被“抹去”，因此保证了输入数据分布稳定在一定范围内。另外，权重的缩放并不会影响到对 $u$ 的梯度计算；

当权重越大时，即 $a$ 越大， $\frac{1}{a}$ 越小，意味着权重 $W$ 的梯度反而越小，这样BN就保证了梯度不会依赖于参数的scale，使得参数的更新处在更加稳定的状态。

因此，在使用Batch Normalization之后，抑制了参数微小变化随着网络层数加深被放大的问题，使得网络对参数大小的适应能力更强，此时我们可以设置较大的学习率而不用过于担心模型divergence的风险。

（3）BN允许网络使用饱和性激活函数（例如sigmoid，tanh等），缓解梯度消失问题

在不使用BN层的时候，由于网络的深度与复杂性，很容易使得底层网络变化累积到上层网络中，导致模型的训练很容易进入到激活函数的梯度饱和区；通过normalize操作可以让激活函数的输入数据落在梯度非饱和区，缓解梯度消失的问题；另外通过自适应学习 $\gamma$ 与 $\beta$ 又让数据保留更多的原始信息。

（4）BN具有一定的正则化效果

在Batch Normalization中，由于我们使用mini-batch的均值与方差作为对整体训练样本均值与方差的估计，尽管每一个batch中的数据都是从总体样本中抽样得到，但不同mini-batch的均值与方差会有所不同，这就为网络的学习过程中增加了随机噪音，与Dropout通过关闭神经元给网络训练带来噪音类似，在一定程度上对模型起到了正则化的效果。

另外，原作者通过也证明了网络加入BN后，可以丢弃Dropout，模型也同样具有很好的泛化效果。

适用场景

在神经网络训练时遇到收敛速度很慢，或梯度爆炸等无法训练的状况时可以尝试BN来解决。

另外，在一般使用情况下也可以加入BN来加快训练速度，提高模型精度。

BN 在每个 mini-batch 比较大，数据分布比较接近的场景比较适用。

在进行训练之前，要做好充分的shuffle，否则效果会差很多。

另外，由于BN需要在运行过程中统计每个mini-batch的一阶统计量和二阶统计量，因此不适用于动态的网络结构和RNN网络。

python实现

参数初始化

$\beta$ 初始化值为0， $\gamma$ 初始化值为1

更新策略

参数更新策略：

$\mu _{statistic+1}=(1-momentum)*\mu _{statistic}+momentum*\mu _{now} \\ \sigma _{statistic+1}^{2}=(1-momentum)*\sigma _{statistic}^{2}+momentum*\sigma _{now}^{2}$

在pytorch中对当前批次feature进行bn处理时所使用的 $\sigma _{now}^{2}$ 是总体标准差，计算公式如下：

$\sigma _{now}^{2}=\frac{1}{m}\sum_{i=1}^{m}(x_{i}-\mu _{now})^{2}$

在更新统计量 $\sigma _{statistic}^{2}$ 时采用的是 $\sigma _{now}^{2}$ 是样本标准差，计算公式如下：

$\sigma _{now}^{2}=\frac{1}{m-1}\sum_{i=1}^{m}(x_{i}-\mu _{now})^{2}$

两种实现方式

验证是否和使用官方bn处理方法结果一致。

第一种：

在bn_process中计算输入batch数据的每个维度（这里的维度是channel维度）的均值和标准差（标准差等于方差开平方）。

然后通过计算得到的均值和总体标准差对feature每个维度进行标准化，然后使用均值和样本标准差更新统计均值和标准差。

def bn_process(x, mean, var):
    b, c, w, h = x.shape
    # 对每个通道进行BN
    for i in range(c):
        x_c = x[:, i]
        mean_c = x_c.mean()
        std_1 = x_c.std()  # 总体方差
        std_2 = x_c.std(ddof=1)  # 样本方差（无偏估计

        x[:, i] = (x[:, i] - mean_c) / np.sqrt(std_1 ** 2 + 1e-5)

        mean[i] = mean[i] * 0.9 + mean_c * 0.1
        var[i] = var[i] * 0.9 + (std_2 ** 2) * 0.1  # 使用样本方差进行更行

    print(x)
    
x = torch.randn(2, 3, 2, 2)  # 元素个数等于channel深度
calculate_mean = [0.0, 0.0, 0.0]
calculate_var = [1.0, 1.0, 1.0]   
bn_process(x.numpy().copy(), calculate_mean, calculate_var)

输出如下：

[[[[ 0.77257067 -1.2975506 ]
   [-0.3630766   1.4894383 ]]

  [[-1.8136703  -0.01955615]
   [-0.8204374   0.31605968]]

  [[ 0.6743245   1.4604934 ]
   [-0.369741   -1.151481  ]]]


 [[[ 1.3495055  -1.004653  ]
   [-0.2599011  -0.68633324]]

  [[ 1.35173     1.0199517 ]
   [-0.74816847  0.7140909 ]]

  [[-0.2033853   0.32857594]
   [ 0.95862955 -1.6974164 ]]]]

第二种：

设计为类，并用实例属性来保存一些变量值。

初始化中beta和gamma对应于BN中需要学习的参数，分别初始化为0和1，接下来就是前向传播的实现：

class BN:
    def __init__(self, momentum, eps, num_features):
        """
        初始化参数值
        :param momentum: 追踪样本整体均值和方差的动量
        :param eps: 防止数值计算错误
        :param num_features: 特征数量
        """

        self._mean = 0
        self._std = 1
        self._momentum = momentum
        self._eps = eps  # 防止计算无效
        self._num_features = num_features
        
        # 对应learnable参数beta和gamma，采用pytorch文档中的初始化值
        self._beta = np.zeros(shape=(num_features, ))
        self._gamma = np.ones(shape=(num_features, ))

    def batch_norm(self, x):
        for i in range(self._num_features):
            x_c = x[:, i]
            x_mean = x_c.mean()
            
            x_std_1 = x_c.std()
            x_std_2 = x_c.std(ddof=1)
            
            # 对应mean的更新公式
            self._mean = (1 - self._momentum) * x_mean + self._momentum * self._mean
            self._std = (1 - self._momentum) * x_std_2 ** 2 + self._momentum * self._std

            # 对应论文中计算BN的公式
            x_hat = (x_c - x_mean) / np.sqrt(x_std_1 ** 2 + self._eps)
            x[:, i] = x_hat
            y = self._gamma[i] * x_hat + self._beta[i]  # 恢复数据表达

        print(x)

由于pytorch中的BatchNorm中beta和gamma初始化并不是0和1，为了保证初始化值一样，将自己定义的类的beta和gamm替换为torch初始化的值，进行如下测试：

bn2 = BN(momentum=0.1, eps=1e-5, num_features=3)
bn2._beta = bn.bias.detach().numpy()
bn2._gamma = bn.weight.detach().numpy()
bn2.batch_norm(x.numpy().copy())

输出如下，可以发现两种实现方式的结果是相同的。

[[[[ 0.77257067 -1.2975506 ]
   [-0.3630766   1.4894383 ]]

  [[-1.8136703  -0.01955615]
   [-0.8204374   0.31605968]]

  [[ 0.6743245   1.4604934 ]
   [-0.369741   -1.151481  ]]]


 [[[ 1.3495055  -1.004653  ]
   [-0.2599011  -0.68633324]]

  [[ 1.35173     1.0199517 ]
   [-0.74816847  0.7140909 ]]

  [[-0.2033853   0.32857594]
   [ 0.95862955 -1.6974164 ]]]]

pytorch官方BN处理方法：

1
2
3

bn = nn.BatchNorm2d(3, eps=1e-5)  # 3 = num_features
output = bn(x)
print(output)  # output 与 x的输出值相同

输出如下：

tensor([[[[ 0.7726, -1.2976],
          [-0.3631,  1.4894]],

         [[-1.8137, -0.0196],
          [-0.8204,  0.3161]],

         [[ 0.6743,  1.4605],
          [-0.3697, -1.1515]]],


        [[[ 1.3495, -1.0047],
          [-0.2599, -0.6863]],

         [[ 1.3517,  1.0200],
          [-0.7482,  0.7141]],

         [[-0.2034,  0.3286],
          [ 0.9586, -1.6974]]]], grad_fn=<NativeBatchNormBackward>)