【算法专题】算法设计与分析复习题汇总

五大算法介绍

（一）分治法（divide and conquer method）

是将待求解的原问题划分成k个较小规模的子问题，对这k个子问题分别求解。如果子问题的规模仍然不够小，则再将每个子问题划分为k个规模更小的子问题，如此分解下去，直到问题规模足够小，很容易求出其解为止（子问题求解思路一致），再将子问题的解合并为一个更大规模的问题的解，自底向上逐步求出原问题的解。

（二）动态规划法（dynamic programing method）

动态规划，当前子问题的解将由上一次子问题的解推算出。

动态规划应用于子问题重叠的情况，即不同的子问题具有公共的子子问题。在这种情况下，分治算法会做出许多不必要的工作，它会反复的求解那些公共子问题，而动态规划对每一个子子问题只求解一次，将结果保存到数组中，从而在下次使用时，直接从数组中得到，无需每次求解一个子子问题时都要重复计算公共子子问题。

（三）贪心法（greedy method）

贪心法并不是从整体最优考虑，它**所做出的选择只是在某种意义上的局部最优。**这种局部最优选择并不总能获得整体最优解（Optimal Solution），但通常能获得近似最优解（Near-Optimal Solution）。

（四）回溯法（back track method）

回溯法采用深度优先方法搜索遍历问题的解空间，可以看作是蛮力法穷举搜索的改进。先判断该节点对应的部分是否是满足约束条件，也就是判断该节点是否包含问题的最优解。如果肯定不包含，则跳过对该节点为根的子树的搜索，即所谓的剪枝；否则，进入该节点为根的子树，继续按照深度优先策略搜索。回溯法常常可以避免搜索所有可能的解，所以，适用于求解组合数组较大的问题。

（五）分支限界法（branch and bound method）

分支限界法按广度优先策略遍历问题的解空间，在遍历过程中，对已经处理的每一个结点根据限界函数估算目标函数的可能值，从中选取使目标函数取得极值（极大或极小）的结点优先进行广度优先搜索，从而不断调整搜索方向，尽快找到问题的解。因为界限函数常常是基于问题的目标函数而确定的，所以，分支限界法适用于求解最优化问题。

算法差异

（一）分治法和动态规划法的区别

• 共同点：二者都要求原问题具有最优子结构性质，都将原问题分成若干个子问题，然后将子问题的解合并，形成原问题的解。

• 不同点：动态规划法是将待求解问题分解成若干个相互重叠的子问题，即不同的子问题具有公共的子子问题，而分治法是分解成若干个互不相交的子问题。利用分治法求解，这些子问题的重叠部分被重复计算多次。而动态规划法将每个子问题只求解一次并将其保存在一个数组中，当需要再次求解此子问题时，从数组中获得该子问题的解，从而避免了大量的重复计算。

（二）动态规划法和贪心法的区别

• 共同点：贪心算法和动态规划算法都要求问题具有最优子结构性质。

• 不同点：动态规划法用到之前的最优解，贪心则不是，贪心无法解决动态规划的问题，但是动态规划能解决贪心的问题。虽然能够应用贪心算法一定能够应用动态规划法，但是一般来说，贪心算法的效率高于动态规划法，因而还是应用贪心算法。动态规划算法通常以自底向上的方式解各子问题，而贪心算法则通常以自顶向下的方式进行，以迭代的方式作出相继的贪心选择，每做一次贪心选择就将所求问题简化为规模更小的子问题。

（三）回溯法和分支限界法的区别

• 共同点：一种在问题的解空间树上搜索问题解的算法。

• 不同点：求解目标不同，回溯法的目标是找出解空间树满足约束条件的所有解，而分支限界法的求解目标是尽快地找出满足约束条件的一个解；搜索方法不同，回溯法采用深度优先方法搜索解空间，而分支限界法一般采用广度优先或以最小消耗优先的方式搜索解空间树；对扩展结点的扩展方式不同，回溯法中，如果当前的扩展结点不能够再向纵深方向移动，则当前扩展结点就成为死结点，此时应回溯到最近一个活结点处，并使此活结点成为扩展结点。分支限界法中，每一次活结点只有一次机会成为扩展结点。活结点一旦成为扩展结点，就一次性产生其所有儿子结点；存储空间的要求不同，分支限界法的存储空间比回溯法大得多，当内存容量有限时，回溯法成功的可能性更大。

适用情况

(一) 分治法

• 适用特征：该问题的规模缩小到一定的程度就可以容易地解决；可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质；利用该问题分解出的子问题的解可以合并为该问题的解；所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子子问题。

• 典型代表：二分搜索、棋盘覆盖、合并排序、最接近点对问题、循环赛日程表、汉诺塔…

(二) 动态规划法

• 适用特征：该问题问题的最优解所包含的子问题的解也是最优的，即满足最优化原理；某状态以后的过程不会影响以前的状态，只与当前状态有关；子问题之间是不独立的，当前子问题的解将由上一次子问题的解推算出。

• 典型代表：最长公共子序列、最优二叉查找树、近似串匹配问题、背包问题、…

(三)贪心法

• 适用特征：该问题局部最优策略能导致产生全局最优解（贪心算法适用的情况很少）。

• 典型代表：TSP问题（最近邻点）、TSP问题（最短链接）、图着色、多极度调度问题…

(四)回溯法

• 适用特征：该问题是求解组合数量较大；需要找出该问题的解集（全部解）或者要求回答什么解是满足某些约束条件的最优解。

• 典型代表：哈密顿回路问题、八皇后问题、批处理作业调度…

(五)分支限界法

• 适用特征：求解最优化问题。

• 典型代表：单源最短路径问题、批处理作业调度问题、电路布线问题

简答题

1. 动态规划与分治算法的异同点

• 共同点 ：二者都要求原问题具有最优子结构性质，都是将原问题分而治之，分解成若干个规模较小(小到很容易解决的程序)的子问题。然后将子问题的解合并，形成原问题的解.

• 不同点：分治法将分解后的子问题看成相互独立的，通过用递归来做。

动态规划将分解后的子问题理解为相互间有联系,有重叠部分，需要记忆，通常用迭代来做。

问题特征：

最优子结构：当问题的最优解包含了其子问题的最优解时，称该问题具有最优子结构性质。

重叠子问题：在用递归算法自顶向下解问题时，每次产生的子问题并不总是新问题，有些子问题被反复计算多次。动态规划算法正是利用了这种子问题的重叠性质，对每一个子问题只解一次，而后将其解保存在一个表格中，在以后尽可能多地利用这些子问题的解。

2. 多项式时间算法

3. 陈述算法在最坏情况下的时间复杂度和平均时间复杂度，这两种评估算法复杂性的方法各自有什么实际意义？

最坏情况下的时间复杂度称最坏时间复杂度。一般不特别说明，讨论的时间复杂度均是最坏情况下的时间复杂度。这样做的原因是：最坏情况下的时间复杂度是算法在任何输入实例上运行时间的上界，这就保证了算法的运行时间不会比任何更长。平均时间复杂度是指所有可能的输入实例均以等概率出现的情况下，算法的期望运行时间。

4. 阐述动态规划算法与贪心算法的区别，它们都有那些优势和劣势？

动态规划算法与贪心算法都要求问题具有最优子结构性质，这是二者的一个共同点。但是对于具有最优子结构的问题应该选择前者还后者来解决？下面通过两个经典的组合优化问题谈谈动态规划算法与贪心算法的主要差异。

动态规划法与分治法和贪心法类似，它也是将原问题分解为若干个更小的、相似的子问题，并通过求解子问题产生一个全局最优解。与分治法和贪心法不同之处在于：

① 使用贪心法时，当前的选择可能要依赖于已经作出的所有选择，但不依赖于有待于做出的选择和子问题。因此贪心法是自顶向下(即从起点到终点)，一步一步地作出贪心选择。当然，如果当前的选择可能要依赖于子问题的解时，则难以通过局部的贪心策略达到全局最优解。

② 使用分治法时，由原问题分解出的各子问题通常是相互独立的，即不包含公共的子问题，因此一旦递归地求出各子问题的解后，便可自下而上地将各子问题的解合并成问题的解。如果各子问题不是相互独立的，则分治法要做许多不必要的工作，重复地求解公共的子问题。

③ 动态规划允许由原问题分解出的子问题之间相互依赖。每一个子问题只求解一次，并将结果保存起来，避免每次碰到此子问题时都要重复计算。

5. 阐述回溯算法与分枝限界算法的共同点和不同点，提高算法效率的关键是什么？

6. 在对算法进行复杂性分析时，强调渐进复杂性的意义是什么？

算法的复杂性是算法效率的度量，是评价算法优劣的重要依据。一个算法的复杂性的高低体现在运行该算法所需要的计算机资源的多少上面，所需的资源越多，我们就说该算法的复杂性越高；反之，所需的资源越低，则该算法的复杂性越低简化算法复杂性分析的方法和步骤，即只要考察当问题的规模充分大时，算法复杂性在渐近意义下的阶。与此简化的复杂性分析方法相配套，问题复杂程度和规模的线性增长导致的时耗的增长和空间需求的增长，对低效算法来说，都是超线性的，决非计算机速度和容量的线性增长带来的时耗减少和存储空间的扩大所能抵销。

7. 简述N类、NP类与NP完全问题的定义及三者之间的关系？

在了解P问题，NP问题，NPC问题以及NP Hard问题之前，我们需要明白多项式级的复杂度和非多项式级的复杂度。时间复杂度是当问题规模扩大后，程序需要的时间长度增长得有多快。有O(1)的时间复杂度，也称常数级复杂度；数据规模变得有多大，花的时间也跟着变得有多长，这个程序的时间复杂度就是O(n)。数据扩大2倍，时间变慢4倍的，属于O(n^2)的复杂度。

• 多项式级的复杂度，它的规模n出现在底数的位置；

• 非多项式级的复杂度，比如O(a^n)和O(n!)型复杂度，其复杂度计算机往往不能承受。

  P问题：如果一个问题可以找到一个能在多项式的时间里解决它的算法，那么这个问题就属于P问题。

  NP问题：在多项式时间内“可验证”的问题。也就是说，不能判定这个问题到底有没有解，而是猜出一个解来在多项式时间内证明这个解是否正确。即该问题的猜测过程是不确定的，而对其某一个解的验证则能够在多项式时间内完成。P类问题属于NP问题，但NP类问题不一定属于P类问题。所有的P类问题都是NP问题，因为能多项式地解决一个问题，也就能够在多项式的时间内验证问题的解。

  NP完全问题：约化： 如果能找到这样一个变化法则，对任意一个程序A的输入，都能按这个法则变换成程序B的输入，使两程序的输出相同，那么我们说，问题A可约化为问题B。
  一个问题A可以约化为问题B的含义即是，可以用问题B的解法解决问题A。比如一元一次方程可以约化为一元二次方程，方法为将一元二次方程的二次项系数设为0。约化具有传递性，如果问题A可以约化为问题B，问题B可以约化为问题C，则问题A可以约化为问题C。
  NPC问题： 首先，它得是一个NP问题；然后，所有的NP问题都可以约化到它。

  NP-Hard问题：它满足NPC问题定义的第二条但不一定要满足第一条（就是说，NP-Hard问题要比 NPC问题的范围广）。NP-Hard问题同样难以找到多项式的算法，但它不列入我们的研究范围，因为它不一定是NP问题。

8. 简述蒙特卡罗算法与拉斯维加斯算法的区别

蒙特卡罗是一类随机方法的统称。这类方法的特点是，可以在随机采样上计算得到近似结果，随着采样的增多，得到的结果是正确结果的概率逐渐加大，但在（放弃随机采样，而采用类似全采样这样的确定性方法）获得真正的结果之前，无法知道目前得到的结果是不是真正的结果。拉斯维加斯方法是另一类随机方法的统称。这类方法的特点是，随着采样次数的增多，得到的正确结果的概率逐渐加大，如果随机采样过程中已经找到了正确结果，该方法可以判别并报告，但在但在放弃随机采样，而采用类似全采样这样的确定性方法之前，不保证能找到任何结果（包括近似结果）。

假如筐里有100个苹果，让我每次闭眼拿1个，挑出最大的。于是我随机拿1个，再随机拿1个跟它比，留下大的，再随机拿1个……我每拿一次，留下的苹果都至少不比上次的小。拿的次数越多，挑出的苹果就越大，但我除非拿100次，否则无法肯定挑出了最大的。这个挑苹果的算法，就属于蒙特卡罗算法——尽量找好的，但不保证是最好的。而拉斯维加斯算法，则是另一种情况。假如有一把锁，给我100把钥匙，只有1把是对的。于是我每次随机拿1把钥匙去试，打不开就再换1把。我试的次数越多，打开（最优解）的机会就越大，但在打开之前，那些错的钥匙都是没有用的。这个试钥匙的算法，就是拉斯维加斯的——尽量找最好的，但不保证能找到。

• 蒙特卡罗算法 ：采样越多，越近似最优解；

• 拉斯维加斯算法：采样越多，越有机会找到最优解；

这两类随机算法之间的选择，往往受到问题的局限。如果问题要求在有限采样内，必须给出一个解，但不要求是最优解，那就要用蒙特卡罗算法。反之，如果问题要求必须给出最优解，但对采样没有限制，那就要用拉斯维加斯算法。

课后作业整理

第三章

3.1 YY and Card


解题思路：

这题可以参考Leetcode的第494题。
我们用 f[i][j] 表示用数组中的前 i 个元素，组成和为 j 的方案数。考虑第 i 个数 nums[i]，它可以被添加 + 或 -，因此状态转移方程如下：f[i][j] = f[i-1][j-nums[i]] + f[i-1][j+nums[i]]

打表过程如下，第 i 行的结果由第 i-1行转移而来。

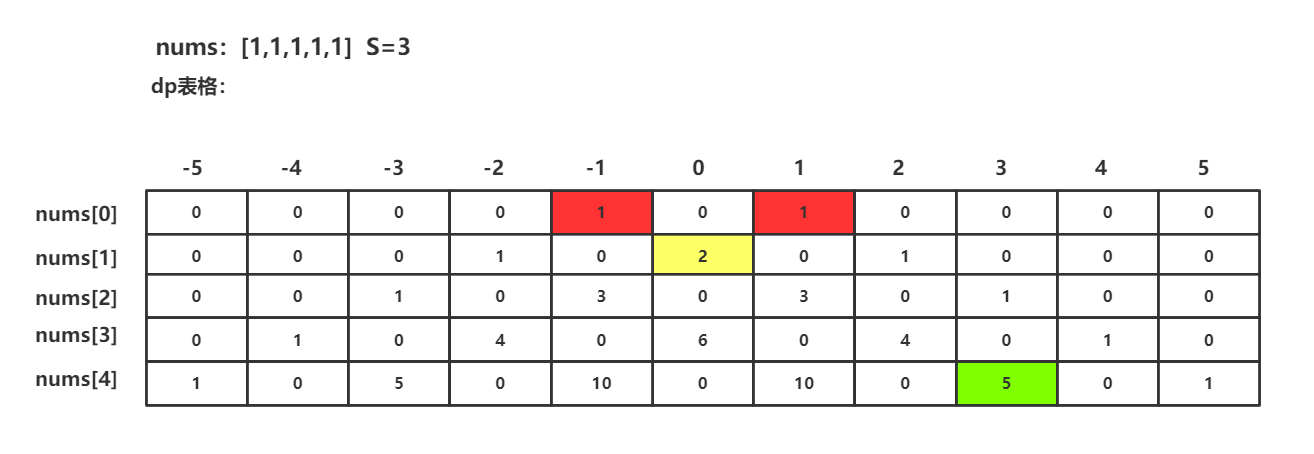
在考虑初始化时要注意，如果nums[0]!=0，红色格子要初始化为1，代表的是，当只有一本书的时候，满足目标和的情况只有一种，即+nums[0]或者-nums[0]。一个需要注意的坑是，如果此时的nums[0]=0，f[0][0]需要初始化为2。因为数组下标是没有复数的，所以应该将第二维的下标进行平移，考虑到总和不超过1000，所以第二维要加上1000。

上述过程可以借助下列代码完成：

f[0][nums[0] + 1000] = 1;
f[0][-nums[0] + 1000] ++;

所以综合下来，代码是这样的：

class Solution {
public:
    int f[21][2002];
    int findTargetSumWays(vector<int>& nums, int S) {
        if (S > 1000) return 0;  // 越界
        f[0][nums[0] + 1000] = 1;
        f[0][-nums[0] + 1000] ++;

        for (int i = 1; i < nums.size(); i++) {
            for (int j = -1000; j <= 1000; j++) {
                if (f[i - 1][j + 1000] > 0) {  // 只计算上一行大于0的情况
                    f[i][j + 1000 - nums[i]] += f[i - 1][j + 1000];
                    f[i][j + 1000 + nums[i]] += f[i - 1][j + 1000];
                }
            }
        }
        return f[nums.size() - 1][S + 1000];
    }
};

3.1 YY and Fab

解题思路：

本题使用二维数组来记录状态，dp[r][s] 表示由区间 f[r] 和 f[s] 组成的斐波那契数列，理论上任何两个数字都可以组成斐波那契数列所以初始化为2：

vector<vector<int>> dp(f.size(), vector<int>(f.size(), 2))

如果存在f[l]+f[r]==f[s] ，就表示存在差值可把两个元组连接起来，故状态转移方程可更新为
dp[r, s] = dp[l, r] + 1

故详细代码如下：

int Fib(vector<int>& F) {
	vector<vector<int>> dp(f.size(), vector<int>(f.size(), 2))
	int ans = 0;
  
  // 固定s端
  for (int s = 2; s < f.size(); s++) {
    int l = 0, r = s - 1;  // l 表示左边界，r 表示右边界
    while (r > l) {
      if (f[l] + f[r] < f[s]) l++;
      else if (f[l] + f[r] > f[s]) r--;
      else {
        dp[r][s] = max(dp[r][s], dp[l][r] + 1);  // 状态转移方程
        ans = max(ans, dp[r][s]);
        l++, r--;
      }
    }
  }
  return ans;
}

3.3 YY and Inverse

解题思路：

dp[i][j]表示1到i的全排列中有 j 个逆序对的排列个数，若已知1...i-1的全排列，将 i 放在全排列的任意位置。

当 i 放到最后一个位置，增加了0个逆序对，故要知道dp[i-1][j-0]

当 i 放到倒数第二个位置，增加了1个逆序对，故要知道dp[i-1][j-1]

…

当 i 放在第一个位置，增加了 i-1 个逆序对，故要知道dp[i-1][j-(i-1)]
所以dp[i][j] = dp[i - 1][j] + dp[i - 1][j-1] + ... + dp[i - 1][j - i + 1]，时间复杂度$O(n² * t)$。

int main() {
  int n, t;
  int M = 1000000007;
  cin >> n >> t;
  int dp[n + 1][t + 1];
  memset(dp, 0, sizeof(dp));
  dp[1][0] = 1;
  for (int i = 2; i <= n; i++) {
    dp[i][0] = 1; // 1到i的全排列逆序对为0的全排列个数有1个（即正序
    for (int j = 1; j <= t; j++) {
      dp[i][j] = (dp[i][j-1] + dp[i-1][j]) % M;
      if (j >= i) {  // 只有当 j - i >= 0 即 j >= i时，最后一项才有值，需要减去
        dp[i][j] = (dp[i][j] - dp[i-1][j-i] + M) % M;
      }
    }
  }
  cout << dp[n][t];
  return 0;
}

3.4 YY and Shop I

解题思路：在不考虑有物品不能购买的情况下，这道题是一个多重背包问题。即有n个物品和一个容量（最大资金）为M（本题的m设为xi的最大值）的背包，第i件物品的体积（促销价）、价值（原价）、数量（限购数量）分别为we[i]、val[i]、num[i]。求解将哪些物品装入背包可使得这些物品的耗费的总空间不超过背包容量，且价值总和最大。
在本题中，当存在物品无法装入时，共有q次询问，每次询问给出了资金xi（1<=xi<=M）和不能购买的物品编号yi。对于单次询问xi，yi，可以把xi拆成两个部分,第yi个禁买，那么花费c购买前y-1个物品，花费x-c购买后y+1个物品。

详细代码如下：

3.5 YY and shop II

/*
先虚构出0节点，那么这就是一个完整的树。
约束是只有得到父节点，才能得到子节点。
参考依赖背包的做法，使用邻接表保存这棵树
但是本题中没有背包容量约束，只是限定取个数，因此每次都取价值最大的商品
动态规划使用 F[父节点][个数]：在购买了当前父节点情况下，再买m-1个子节点商品所能得到的最大价值
里对于树中的每个节点来说，就是一个分组背包问题。每个子节点是一组物品。 
我们从叶子节点往上到根节点规划，当规划到 0 节点时，F[0][m]即为我们所求 
	
邻接表
	假设有一棵树如下： 
		    0 
		1   2   3
 	  4 5	6  7 8

	用邻接表可以写成
	 H   NE
	 0   3 2 1 -1
	 1   5 4 -1
	 2   6 -1
	 3   8 7 -1
	 4   -1
*/ 
#include<bits/stdc++.h> 
using namespace std;
int N,M; //物品件数，每人限购个数 
int H[301], NE[301]; //用邻接表保存树结构，H保存邻接表的头，NE是有共同起点下的另一条边 
int W[301]; //物品的价值 
int F[301][301]; //前一维存放父节点、后一维存放每人限购件数 


void dfs(int p){
	for(int i=H[p]; i!=-1; i=NE[i]){ //p是父节点商品序号，所有i都是其子节点商品序号 
		dfs(i);
		for(int m=M; m>=1; --m){//因为要留出一个买父节点p的物品，所以只能分配出2~m个给子节点商品 
			for(int m2=0; m2<=m; ++m2){ //接着再分，每个子节点能得到的分配到的个数是m2 
				F[p][m]=max(F[p][m], F[p][m-m2]+F[i][m2]);
			}
		} 
	}
    for(int m=M; m>=1; --m) F[p][m] = F[p][m-1]+W[p]; //这里要加上P节点的价值哦 
} 

int main(){
	cin>>N>>M;
	
	//构建邻接表 
	memset(H, -1, sizeof(H)); 
	int p; 
	for(int i=1; i<=N; ++i){
		scanf("%d%d",&p,&W[i]);
		NE[i]=H[p];
		H[p]=i;	
	}

	W[0]=0;//虚构0节点
	++M; //因为加上虚构节点，所以购买个数要加1 
	memset(F, 0, sizeof(F));
	dfs(0);
	
	cout<<F[0][M]<<endl;
	return 0;
}

第五章

5.1 小明爱数数

#include<iostream>
#include<vector>
#include<queue>
#include<string>

using namespace std;
int n;
int v[1000010]; // v记录的是 余数

/*
 参考思路：两个数的前缀模一个数的结果相等时，最终结果是否相等由其后缀唯一决定
         由于数值从小到大遍历，那么在取余过程中，有一个余数第二次出现时，
         这个数往后延伸出来的数都是没有意义的，因为它肯定不是最小的n的倍数
 */

struct node {
    string str;  // 字符串
    int num;  // 该字符串转化为数字后 模n得到的结果
};

void bfs() {
    queue<node> que;
    node p, q;
    
    p.str = "1";
    p.num = 1 % n;
    
    v[p.num] = 1; // 判断的数值从 1 开始
    que.push(p);
    
    while( !que.empty() ) {
        p = que.front();
        que.pop();
        if (p.num == 0) {   // 表示该数可以被整除
            cout << p.str;
        }
        // 加 0
        q.str = p.str + '0';
        q.num = (p.num * 10) % n;  // 直接处理余数即可，将余数乘10后再计算
        
        if ( !v[q.num] ) {
            v[q.num] = 1;
            que.push(q);
        }
        
        // 加 1
        q.str = p.str + '1';
        q.num = (p.num * 10 + 1) % n;  // 直接处理余数即可，将余数乘10 + 1后再计算
        
        if ( !v[q.num] ) {
            v[q.num] = 1;
            que.push(q);
        }
    }
}

int main() {
    cin >> n;
    bfs();
    return 0;
}

5.2 小明与序列

解题思路：

用树的左右结点表示，选不选这个数，结点的值表示当前的序列和，叶节点就是所有的子序列的和。用优先队列存储当前前k小序列和，当队列长度小于k时，直接加入叶子节点值，当队列长度等于k时，比较当前叶子结点值和优先队列队首的值，若小于，则将队首出队，当前叶子结点值加入优先队列。

剪枝时，比较当前序列和和优先队列队首的值，若大于等于则剪枝。可先将序列按从大到小排序，让序列和小的尽可能先出现。

关键代码如下：

void back(int m, long long ans) {
  if (q.size() == k) {
    if (ans >= q.top()) return;  // 剪枝
  }
  // m = n时 表明到达叶节点
  if (m == n) {
    if (ans == 0) return;
    if (q.size() < k) q.push(ans);
    else if (ans < q.top()) {  // 值更小
      q.pop();
      q.push(ans);
    }
    return;  // 回溯
  }
  back(m+1, ans);
  back(m+1, ans + a[m]);
}

5.3 小明坐地铁

解题思路：

1. 用树的左右结点表示，下一个站点在上一个站点的左边还是右边，结点的值表示站点所在的位置，假设a0站点在位置0，即有Backtrack(0, 0)开始，两个0分别表示第i站的坐标为j。
2. 通过判断每条到叶子结点的路径上有多少个值不同的点，来得到站点最小可能是多少。
3. 到叶子结点时，比较当前站点数与当前最小站点数，选择较小的。
4. 当前的站点数若已经大于当前最小站点数，则剪枝

关键代码如下所示：

void distant(int n, int site) {
  if (n - 1 == m) {
    if (num < minn) minn = num;
    return;
  }
  if (num >= minn) return;  // 剪枝
  if (x[site + N] == 0) num++;  // 没有来过的站点
  x[site + N] ++;
  distance(n + 1, site + a[n]);  // 回溯
  distance(n + 1, site - a[n]);
  if (x[site + N] == 1) num--;  // 恢复现场
  x[site + N] --;
}

5.4 小明和最小点覆盖

解题思路：

使用两个数组x和y来代表每条边对应的两个端点，使用visited数组来代表某个端点是否被访问过，即是否加入了结果集。

遍历无向图中的所有边：

• 如果某条边的两个端点之一被访问过了，则表明该边所连接的两个点已经有一个点被选到了，则该边连接的另一个点就不需要加入结果集，这时候就遍历下一条边，但结果集中的点数不增加。
• 如果某条边的两个端点都没被访问过，则需要选取该边中的任意一个端点加入结果集，结果集中的点数加一，遍历下一条边。
• 重复(1)，(2)步骤，直至遍历完所有边或者当前结果集超过了最小结果集。

关键代码如下：

void dfs(int t, int temp) {
  // 递归出口
  if (temp > n) return;
  if (t == m) {
    ans = temp;
    return;
  }
  
  if (temp < ans) {
    // if 表示 两端的点均未被选中的情况
    if (node[edge[t][0]] == 0 && node[edge[t][1]] == 0) {
      for (int j = 0; j < 2; j++) {
        node[edge[t][j]] = 1;
        dfs(t + 1, temp + 1);
        node(edge[t][j]) = 0;
      }
    } else {  // 点已经被选中了
      dfs(t + 1, temp);
    }
  }
}

5.5 小明和第K小带权匹配

1. 对边进行搜索，搜索出所有的匹配可能性及其所对应的权重值，从小到大进行排序取出第k项。
2. 由于只需要知道第k小的数，所有比第k项大的数据都没有用，因此只需要存储前k小的数，在搜索树上所有当前节点权值大于k的子树可全部舍弃。
3. 精心设计的数据可能导致搜索过程中权值从最大到最小依次递减，可先对边进行从小到大的排序降低搜索空间。

关键代码如下：

void dfs(int t, int sum, int* Lef, int* Rit) {
    //表示所有的边都已经枚举完了
    if(t == m || Count == k || sum+Em[t].w > mid) return ;
   //表示左或右此节点已经有边了--强剪枝
    if(Lef[Em[t].u] != 1 && Rit[Em[t].v] != 1){ 
        Count++;//选择 
        Lef[Em[t].u] = 1;
        Rit[Em[t].v] = 1;
        dfs(t+1, sum + Em[t].w, Lef, Rit);
        Lef[Em[t].u] = 0;
        Rit[Em[t].v] = 0;
    }
    dfs(t+1, sum, Lef, Rit);
}