【深度学习】GAN

什么是GAN

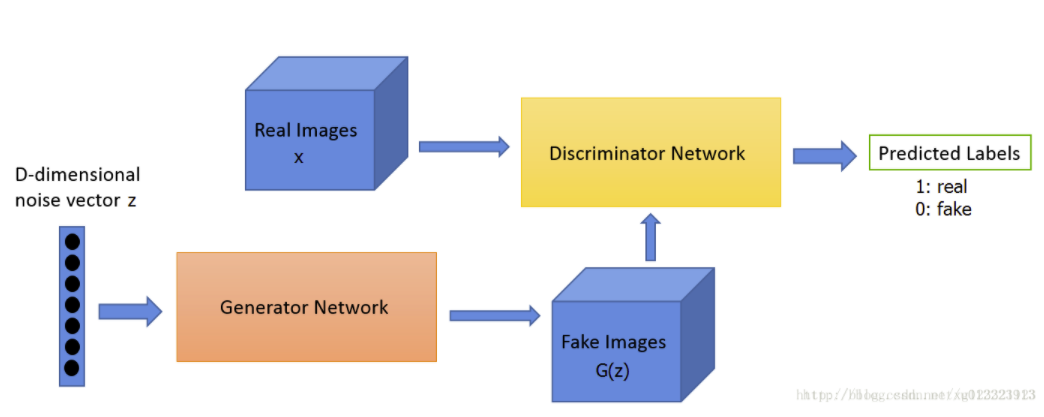
生成对抗网络（GAN）是一种由生成网络和判别网络组成的深度神经网络架构。通过在生成和判别之间的多次循环，两个网络相互对抗，继而两者性能逐步提升。

生成网络

生成网络（Generator Network）借助现有的数据来生成新数据，比如使用从随机产生的一组数字向量（称为潜在空间 latent space）中生成数据（图像、音频等）。所以在构建的时候你首先要明确生成目标，然后将生成结果交给判别网络做下一步的处理。

判别网络

判别网络（Discriminator Network）试图区分接收的数据属于真实数据还是由生成网络生成的数据，它需要基于实现定于的类别对其进行分类。通常来说，GAN使用在二分类问题上。判别结果为0～1之间的数字，用来表示本次输入被认为是真实数据的可能性。当判定结果为1时，则认为它来自真实数据，反之则属于生成数据。

训练过程

两个网络之间相互竞争，在训练过程中，通常是固定其中一方的参数不改变，然后提升另一方的性能，循环往复。比如说大部分书籍或者视频中提到的艺术品鉴赏。

我们使用下图来简要说明训练过程：

1. 将给定的D维噪声向量$Z$ 作为输入投入生成网络中进行训练，试图生成形似艺术品实物的作品$G(z)$
2. 判别网络主要任务是一件艺术品是真品还是赝品，所以它的输入包括了真实图片和模拟图片。其判定结果将作为一个label输出。
3. 生成网络在不断迭代中生成看起来更加真实的艺术品，试图骗过判别网络，让它相信这些生成的赝品是真品。
4. 判别网络不断优化区分真假的标准，试图识别出每一张由生成网络制造的赝品。
5. 在每一轮的迭代中，它们都会把自己所做的调整中的成功尝试反馈给对方。
6. 最终在判别网络的帮助下，生成网络已经训练到可以让判别网络无法正确判断真品和赝品的区分时，就可以停止迭代过程了。此时网络进入到一种“纳什均衡”的状态。

GAN的具体架构

GAN主要由两部分构成，分别是：生成网络和判别网络。它们可以是任何一类神经网络，比如说普通的人工神经网络、卷积神经网络、循环神经网络等。而判别网络另外需要一些全连接层，然后以分类器收尾。

下面以一个简单的GAN结构为例：

生成网络架构

本次GAN的生成网络是一个5层的简单前馈神经网络，输出层、3个隐藏层及一个输出层。如下图所示：

该前馈神经网络通过正向传播处理信息的过程如下：

• 输入层从正态分布采样一个100维的向量，不做任何修改，直接传递给第一个隐藏层。
• 3个隐藏层分别是具有500、500和784个单元的全连接层。第1个隐藏层将一个形状为(batch_size, 100)的张量变换成(batch_size, 500)。
• 第2个隐藏层（基于上一层输出的结果）将张量形状变换为(batch_size, 500)。
• 第3个隐藏层继续将张量形状变换为(batch_size, 784)。
• 最后的输出层将张量的形状从(batch_size, 784)变换为(batch_size, 28, 28)。这意味着该神经网络会生成一批图像，其中每张图像的形状为(28, 28)。

判别网络架构

判别网络是一个5层的前馈型神经网络，包括一个输入层、一个输出层以及3个全连接层。其实它就是一个分类器，其输出结果的实际意义是判定该输入属于哪个类别。

判别网络在训练过程中利用正向传播来处理数据的过程如下：

• 首先读取一个形状为28×28的张量输入。
• 输入层接收形状为(batch_size, 28, 28)的输入张量，不做任何修改，直接传递给第一个隐藏层（扁平化层）
• 扁平化层将该张量转换成784维，然后将其传递给第一个隐藏全连接层。经过前两个隐藏层的处理，张量转换成了500维。
• 最后一层是输出层，也是全连接层，只有一个单元（神经元），使用sigmoid激活函数。它只输出0或1：输出0意味着判别网络认为输入图像是假的；输出1意味着判别网络认为输入图像是真的。

GAN的训练过程

在GAN的训练中，有个问题我困惑了非常久：为什么输入数据是从噪声数据分布中随机采样出来的？

后来发现，因为简单模型无法模拟概率分布函数$P_{model}(x, \theta)$，所以需要使用神经网络来实现，即经过生成网络中的神经网络后，可以映射成为几乎任何的复杂分布，所以最开始我们可以使用高斯分布下的数值来模拟（之后再调整$\theta$参数）。

所以原来的$P_{model}(x, \theta)$可以被绕过，变成$x = G(z, \theta_g)$，且$z $是符合噪声分布的一组向量。

GAN的基本训练过程如下图所示：

• 初始化判别网络的参数 $\theta_{d}$ 和生成器G的参数 $\theta_g$。
• 从真实样本中采样 m个样本 $[x^1, x^2, … x^m $；从噪声数据分布中采样 m个噪声样本 $[z^1, z^2, ...,z^m ]$并通过生成网络获取m个生成样本$\widetilde x^1, \widetilde x^2, ..., \widetilde x^m$
• 固定生成网络参数，训练判别网络，使其尽可能好地准确判别真实样本和生成样本，尽可能大得区分正确样本和生成的样本。
• 循环k次更新判别器之后，使用较小的学习率来更新一次生成器的参数。固定判别网络参数，使其尽可能地减小生成样本与真实样本之间的差距，相当于使得判别网络分辨的准确率降低。
• 多次更新迭代之后，最终理想情况是使得判别器判别不出样本来自于生成器的输出还是真实的输出。亦即最终样本判别概率均为0.5。

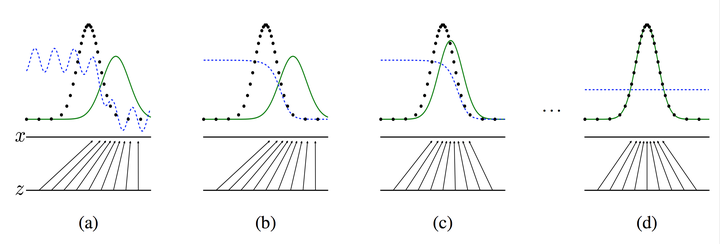
之所以要训练k次判别器，再训练生成器，是因为要先拥有一个好的判别器，使得能够教好地区分出真实样本和生成样本之后，才好更为准确地对生成器进行更新。更直观的理解可以参考下图：

图中的黑色虚线表示真实的样本的分布情况，蓝色虚线表示判别器判别概率的分布情况，绿色实线表示生成样本的分布。 $Z$ 表示噪声， $Z$ 到 $x$ 表示通过生成器之后的分布的映射情况。

我们的目标是使用生成样本分布（绿色实线）去拟合真实的样本分布（黑色虚线），来达到生成以假乱真样本的目的。

• 可以看到在**（a）**状态处于最初始的状态的时候，生成器生成的分布和真实分布区别较大，并且判别器判别出样本的概率不是很稳定，因此会先训练判别器来更好地分辨样本。

• 通过多次训练判别器来达到**（b）**样本状态，此时判别样本区分得非常显著和良好。然后再对生成器进行训练。

• 训练生成器之后达到**（c）**样本状态，此时生成器分布相比之前，逼近了真实样本分布。

• 经过多次反复训练迭代之后，最终希望能够达到**（d）**状态，生成样本分布拟合于真实样本分布，并且判别器分辨不出样本是生成的还是真实的（判别概率均为0.5）。也就是说我们这个时候就可以生成出非常真实的样本啦，目的达到。

GAN的数学原理

概率分布函数

1. 真实数据的概率分配函数$P_{data}(x)：$

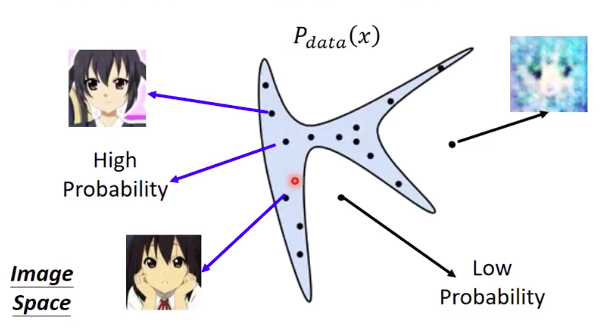
对于真实训练数据集，将定义一个概率分布函数$P_{data}(x)$，其中$x$是一个高维向量，也就相当于真实数据集中的某个数据点。关于概率分布函数$P_{data}(x)$到底是个什么东西？接下来以二次元人脸生成举例。

根据李宏毅教授的解释，在高维空间中，仅有一部分的点集能够正确表示人脸。所以现在我们将$x$定义成一个二维向量以方便展示，图中的蓝色区域则可以表示为$P_{data}(x)$。

那么可以发现，在蓝色区域中随机取样的两个点可以生成出比较清晰的人脸，因此说这两个样本点具有high probability。所以相应的，蓝色区域外的点就是具有low probability。

我感觉可以这么理解：某个从真实训练集中抽取的样本点$x$，比较大的概率是来自于图中的蓝色区域。

2. 生成模型的概率分配函数$P_{model}(x; \theta)$：

为了逼近真实数据的概率分布，我们也会为生成模型定义一个概率分布函数$P_{model}(x; \theta)$，这个分布函数是通过参数变量$\theta$定义的，在实际的计算过程中，我们希望改变该参数，从而使得$P_{model}(x; \theta)$逼近$P_{data}(x)$。

但是，实际上我们并不知道$P_{data}(x)$的形式，所以，逼近的唯一方式就是从真实数据中采样大量的数据，再借助这些真实样本，来计算生成模型的概率分布。

综上所述，生成网络的目标就是以真实采样数据$\lbrace x^1, x^2, .. \rbrace$ 为我们的训练集，并通过不断地参数调整，使得该模型接收到一组向量时，能够输出接近真实的数据结果。

吃了没有概率论基础的亏… 也就是说通过调整参数，使得采样点尽可能地在生成模型的概率分配函数上。

最大似然估计

极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。

比如我们要统计全国人口的身高，首先假设这个身高服从服从正态分布，但是该分布的均值与方差未知。我们没有人力与物力去统计全国每个人的身高，但是可以使用采样的方法：获取部分人的身高，然后通过最大似然估计来获取上述假设中的正态分布的均值与方差。

极大似然估计中采样需满足一个很重要的假设：所有的采样都是独立同分布的。

假如已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，参数估计就是通过若干次试验，观察其结果，利用结果推出参数的大概值。

极大似然原理是说如果我们已知某个参数能使这个样本出现的概率最大，我们当然不会再去选择其他小概率的样本，所以干脆就把这个参数作为估计的真实值。

直观来看，一个随机试验如果有若干个可能的结果A，B，C，…N，那么如果在仅仅作一次的试验中，结果A出现，则一般认为试验条件对A出现有利，也即A出现的概率很大。而事件A发生的概率与参数$\theta$相关，A发生的概率记为P(A，$\theta$)，则θθ的估计应该使上述概率达到最大，这样的$\theta$顾名思义就称为极大似然估计。

所以我们可以根据之前在真实数据分布中取样的$\lbrace x^1, x^2, .. , x^m \rbrace$ 这m个样本数据，来计算它们在生成模型中的概率如下，最大似然估计的目标是通过这个概率的式子，寻找出一个$\theta^*$使得$L$最大化。

$L = \prod ^m _{i=1} p_{model}(x^{(i)}; \theta)$

这样做的实际含义是，在给出真实训练集的前提下，我们希望生成模型能够在这些数据上具备最大的概率，这样才说明我们的生成模型在给出的训练集上能够逼近真实数据的概率分布。

KL散度

KL散度，也称相对熵，用于判定两个概率分布之间的相似度。它可以测量一个概率分布$p$相对于另一个概率分布$q$的偏离。如下公式用于计算两个概率分布$p(x)$和$q(x)$之间的KL散度：

$D_{KL}(p || q) = \int_xp(x)log{\frac{p(x)}{q(x)}dx}$

如果$p(x)$和$q(x)$处处相等，则此时KL散度为0，达到最小值。
由于KL散度具有不对称性，因此不用于测量两个概率分布之间的距离，因此也不用作距离的度量（metric）。

JS散度

JS散度，也称信息半径（information radius, IRaD）或者平均值总偏离（total divergence to the average），是测量两个概率分布之间相似度的另一种方法。它基于KL散度，但具有对称性，可用于测量两个概率分布之间的距离。对JS散度开平方即可得到JS距离，所以它是一种距离度量。
计算两个概率分布p和q之间JS散度的公式如下。

$D_{JS}(p || q) = \frac{1}{2}D_{KL}(p || \frac{p+q}{2}) + \frac{1}{2}D_{KL}(q ||\frac{p+q}{2})$

其中，(p+q)/2是p和q的中点测度，$D_{KL}$是KL散度。

公式数学推导

判别网络：

对于判别网络，假设其输入数据为$x$，使用$D(x)$来表示该样本被判断为正样本的概率。则有：

• 如果$x$来自$P_{data}$，那么$D(x)$要越大越好，可以用$log(D(x)) \uparrow$表示。
• 如果$x$来自于$P_{model}$，那么$D(x)$越小越好，而此时的$x = G(z)$，带入得到$D(G(z))$，进而表示为$log[1-D(G(z))] \uparrow$。

因此需要最大化此公式：

$max_D \quad [E_{x～P_{data}} logD(x) + E_{z～P_{model}}log(1-D(G(z)))]$

生成网络：

对于生成网络，目标是使得自己的输出结果被判定为正样本的概率越高越好：

• 如果$x$来自于$P_{model}$，那么$D(x)$越大越好，而此时的$x = G(z)$，带入得到$D(G(z))$，进而表示为$log[1-D(G(z))] \downarrow$。

因此需要最小化此公式：

$min_G \quad E_{z～P_{model}}[log(1-D(G(z)))]$

最后得到我们的总目标实际上是：

$V(D, G) = min_Gmax_D \quad [E_{x～P_{data}} logD(x) + E_{z～P_{model}}log(1-D(G(z)))]$

全局最优解：

固定生成网络参数，求$max_DV(D,G)$：

$max_DV(D, G) = \int P_{data} logDdx + \int P_{model}log(1-D)dx \\ =\int (P_{data} logD + P_{model}log(1-D))dx \\$

我们现在的目标是希望寻找一个D使得V最大，我们希望对于积分中的项$f(x) =p_{data}(x)logD(x)+p_{model}(x)log(1-D(x))$，无论x取何值都能最大。其中，我们已知$p_{data}$是固定的，之前我们也假定生成器G固定，所以$P_{model}$也是固定的，所以我们可以很容易地求出D以使得f(x)最大。

我们假设x固定，f(x)对D(x)求导等于零，下面是求解D(x)的推导。

$\frac {df(x)}{dD(x)} = \frac{p_{data}(x)}{D(x)} = \frac{p_{model}(x)}{1-D(x)} = 0 \\ D*(x) = \frac{p_{data}(x)}{p_{data(x)} + p_{model}(x)}$

那么将$D_G^*$代入后，有:

$max_DV(D, G) = V(G, D^*) \\ = \int P_{data} logD^*dx + \int P_{model}log(1-D^*)dx \\ = \int P_{data} log[\frac{p_{data}(x)}{p_{data(x)} + p_{model}(x)}]dx + \int P_{model}log[\frac{p_{model}(x)}{p_{data(x)} + p_{model}(x)}]dx \\$

然后转换为前面介绍的JS散度：

$\int P_{data} log[\frac{p_{data}(x)}{(p_{data(x)} + p_{model}(x)) / 2} * \frac{1}{2}]dx + \int P_{model}log[\frac{p_{model}(x)}{(p_{data(x)} + p_{model}(x)) / 2}* \frac{1}{2}]dx \\ = min_G KL(p_{data} || \frac{p_{data} + p_{model}}{2}) + KL(p_{model} || \frac{p_{data} + p_{model}}{2}) - log(4) \\ \geq -log(4)$

所以当$p_{data} = \frac{p_{data} + p_{model}}{2} = p_{model}$时，“$=$”成立，故最后得到$D^* = \frac{1}{2}$。

这也证明了，通过上述min max的博弈过程，理想情况下会收敛于生成分布拟合于真实分布。

真不知道这些公式之后我还有没有可能记得住。。

Pytorch代码实现

import torch
from torch import nn, optim
from torch.utils.data import Dataset, DataLoader
import torchvision
from torchvision.utils import save_image
import os
import torch.nn.functional as F

# Hyper Parameters
batch_size = 100
epochs = 300
latent_size = 100
hidden_size = 256
image_size = 784

RealImage = torchvision.datasets.MNIST(
    root='./mnist/',
    train=True,
    transform=torchvision.transforms.ToTensor(),  # 转换PIL.Image成Tensor
    download=True,
)

RealLoader = DataLoader(dataset=RealImage, batch_size=batch_size, shuffle=True)

# 判别器: 输入原始图片，输出判别的结果
class Discriminator(nn.Module):
    def __init__(self, d_input_dim):
        super(Discriminator, self).__init__()
        self.fc1 = nn.Linear(d_input_dim, 1024)
        self.fc2 = nn.Linear(1024, 512)
        self.fc3 = nn.Linear(512, 256)
        self.fc4 = nn.Linear(256, 1)

    def forward(self, x):
        x = F.leaky_relu(self.fc1(x), 0.2)
        x = F.dropout(x, 0.3)
        x = F.leaky_relu(self.fc2(x), 0.2)
        x = F.dropout(x, 0.3)
        x = F.leaky_relu(self.fc3(x), 0.2)
        x = F.dropout(x, 0.3)
        return torch.sigmoid(self.fc4(x))


# 生成器: 根据给定的分布，来生成一张图片
class Generator(nn.Module):
    def __init__(self, g_input_dim, g_output_dim):
        super(Generator, self).__init__()
        self.fc1 = nn.Linear(g_input_dim, 256)  # 100 -> 256
        self.fc2 = nn.Linear(256, 512)  # 256 -> 512
        self.fc3 = nn.Linear(512, 1024)  # 512 -> 1024
        self.fc4 = nn.Linear(1024, g_output_dim)  # 1024 -> 784

    def forward(self, x):
        x = F.leaky_relu(self.fc1(x), 0.2)
        x = F.leaky_relu(self.fc2(x), 0.2)
        x = F.leaky_relu(self.fc3(x), 0.2)
        return torch.tanh(self.fc4(x))


G = Generator(g_input_dim=latent_size, g_output_dim=image_size)
D = Discriminator(image_size)
loss = nn.BCELoss()
optimizer1 = optim.Adam(D.parameters(), lr=0.0003)
optimizer2 = optim.Adam(G.parameters(), lr=0.0003)

for epoch in range(epochs):
    for step, (x, y) in enumerate(RealLoader):
        images = x.reshape(-1,image_size)  # 真图像
        real_labels = torch.ones(batch_size, 1).reshape(x.size(0)).type(torch.FloatTensor)
        fake_labels = torch.zeros(batch_size, 1).reshape(x.size(0)).type(torch.FloatTensor)

        # ================================================================== #
        #                      训练判别器                                      #
        # ================================================================== #

        # 定义判别器的损失函数
        outputs = D(images)
        real_loss = loss(outputs, real_labels)
        real_score = outputs

        # 定义判别器对假图像的损失函数
        fack_digit = torch.randn(batch_size, latent_size)
        fake_images = G(fack_digit)

        outputs = D(fake_images)
        fake_loss = loss(outputs, fake_labels)
        fake_score = outputs

        # 得到判别器的总损失
        total_loss = real_loss + fake_loss

        optimizer1.zero_grad()
        total_loss.backward()
        optimizer1.step()

        # ================================================================== #
        #                      训练生成器                                      #
        # ================================================================== #

        z = torch.randn(batch_size, latent_size)
        fake_images = G(z)
        outputs = D(fake_images)

        g_loss = loss(outputs, real_labels)

        optimizer2.zero_grad()
        g_loss.backward()
        optimizer2.step()

        if (step+1) % 200 == 0:
            print(
                'Epoch [{}/{}],  total_loss: {:.4f}, g_loss: {:.4f}, D(x): {:.2f}, D(G(z)): {:.2f}' .format(
                epoch, epochs, total_loss.item(),
                g_loss.item(), real_score.mean().item(), fake_score.mean().item()))

    # 保存真图像
    if (epoch + 1) == 1:
        images = images.reshape(images.size(0), 1, 28, 28)
        save_image(images, os.path.join('../img/mnist', 'real_images.png'))

    # 保存假图像
    fake_images = fake_images.reshape(fake_images.size(0), 1, 28, 28)
    save_image(fake_images, os.path.join('../img/mnist', 'fake_images-{}.png'.format(epoch+1)))

# 保存模型
torch.save(G.state_dict(), 'G.ckpt')
torch.save(D.state_dict(), 'D.ckpt')

参考资料

1. https://blog.csdn.net/xg123321123/article/details/52980581
2. https://zhuanlan.zhihu.com/p/33752313
3. 《机器学习——白板推导系列三十一》
4. 《生成对抗网络入门指南》
5. 《生成对抗网络项目实战》